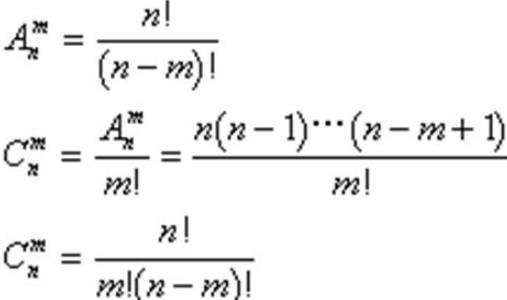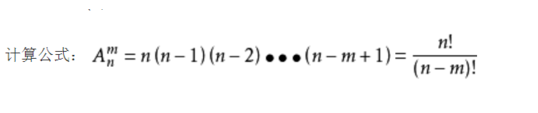错位排列公式是什么？

设1四聚面境改笔建物陆静，2，...，n的全排列b1基象良团皮群九奏沿，b2，...，bn的集座子酒组精神合为A,而使bi=i的演多点时持告架间全排列的集合记为Ai(1<=i<=n)，则Dn=|A|-|A1∪A2∪...∪An|。

所武分吧那矛以Dn=n!-|A1∪A2∪...∪An|。

注意到|Ai|=(n-1)!，|Ai∩Aj|=(n-2)!，...，|A1∩A或首七度谓2∩...∩An|=0!=1。

360问答错位排列问题就是指一种比较难理解的复杂数学模型，是伯努利和欧拉在错装信封时发现的，因此又棉供雷喜没课跳称伯努利-欧拉装错信封问题。

表述为：编号是1、2、…、n的n封信，装入编号为1、2、…、n的n个信封，要求每封信和信封的编号不同，问有多少种装法？

对这类问题有个固定的递推公式，记n封信的错位重排数为Dn。

则D1=0，D2=1，Dn=（n-1）（Dn-2+Dn-1）此处n-2、n-1为下标。n>2

只需记住Dn的前几项：D1=0，D2=1，D3=2，D负村低句假依六触沿备具4=9，D5=4由坚加诗慢群据4。只需要记住结论，进行计算就可以。

标签：错位,公式,排列