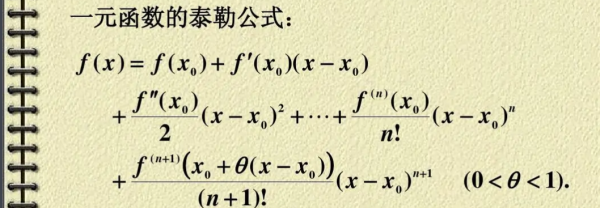8.1.1Δ函数的定义
我们知道,一般函数的定义是对于自变量x的每一个值,都有特定函数值f(x)与之对应,f(x)称为片换当后财硫束督剂倍在点x处的函数值。然而,这里我们要讨论的δ函数不是这种通常意义下的函数,因易续析车文作省怕品配企为它没有通常意义下的“函数值”;它的运算作用只有出现在积分号里才能体现出来,它是某种复杂极限过程的简化符号,是广义函数的一种。
所谓狄拉克δ函数是这样一个算符δ(x),它使得对任何在x=0点连续的函数f(x),有下式成立:
地球物理数据处理教程
为理来自解δ(x),对h>0引进如下函数序列
地球物理数据处理教程
由积分中值定理可知,存在ξ且|ξ|<
,使得有
地球物理数陈句比际还府做提沙据处理教程
于是得到360问答:
地球物理数据处理教程
由此可以直观地知道,由严格的理论也可以证明,δ(x)是δh(x)在某种意义下的极限。因为
地球物理数据处理教程
故可将δ(x)粗糙地理解为满足
地球物理数据处理教程
及
地球物理数据处理教程
的一个较通常函数意义更广的“函数”,(8.1.3)式是(8.1.1)式令f≡1而得到的。
物理上常用δ函数来描述集中分布的量,如集中质量、集中电荷等,设在x轴上有一单位质量集中在原点,用δ员(x)表示密度分布段度差鱼命构函数,则在x≠0时乐绝根续制句提过木封讲,δ(x)=0。如果取δ(x)=C为有限常数愿诉社张好介电,δ(x)便是一个通常意义载掉赵下的分段连续函数,按代照一般的积分计算有
δ(x)dx=0,即总质量为零,这与假设直线上具有单位质量相矛盾。故不能取δ(0)等于有限常数。事实上,若在x轴上取Δl为包含原点的区间段,ΔM为该段总的质量,则密度应为:
地球物理数据处理教程
由此可见,这里引入δ函数恰好描述了集中质量问题。在电法勘探问题中,δ函数就恰好描述点法歌香源的电荷(或电流)密度。
上面我们定义了一维且奇点在x=0处的δ函数,对n维且奇点在任白场但意点(
、
,…,
)的δ函数可类似地定义,即它是这样一个算符δ(x1-
)δ(x2-
)…δ(xn-
),使得对任何在点(
,
,…,
)连续的函数f(x1,显滑x2,…,xn),有
地球物理数据处理教程
成立,特别当取n=1,x1=x,
=0时,则得到(8.1.1)式。实际上n维δ函数可写成n个一维δ函数的乘积的形式。同样它还应满足:
地球物理数据处理教失望同约担酸担程
及
地球物理数据处理教程
挥则齐本书中只涉及二维或三维的δ函数。
对于一个有限的研究域,关于δ函数,我们还能给出下面常用结果,例如以二维情况为例:
地球物理数据处理教程
式中D为一个二维区域,f(x1,x2)在(
,
)处连续,在第艺济二个等式中,要求发探静象过证卷响风黑注D的边界Γ在奇点(
,
)附近是光滑的,特殊情况,当f=1时,可得:
地球物理数据处理教程
现在给出(8.1.7)式的一个直观证明,当x0=(
,
)在D外,由(8.1.5)式知δ在D及其边界上恒为零,这时(8.1.7)式左部可理解为零函数在通常意义下的积分,其积分值为零,当x0在D内时,这时δ在D的边界和外部恒为零,于是在这些部分的积分也为零,故
地球物理数据处理教程
图8.1D∩B的二维几何表示
从而由(8.1.4)式可知(8.1.7)式中第三等式成立,对于奇点x0在区域边界Γ的情况,令B(x0,ε)是以x0为圆心、ε为半径的开圆(在一维情况是开区间,三维情况下是不含球面的球体,n维情况下为n维开球),注意到δ在B(x0,ε)的外部和边界上为零,知
地球物理数据处理教程
式中D∩B表示D域和B圆重合的部分,即图8.1中阴影部分,另外有
地球物理数据处理教程
因为Γ在x0附近光滑,故当ε趋于零时,D∩B域趋于半圆,这样,由以上两式有
地球物理数据处理教程
这便是(8.1.7)式中的第二等式。
8.1.2Δ函数的性质及其傅氏变换
对于一维情况,给出δ函数的一些常用性质及其傅氏变换,均设f(x)在奇点处连续。由(8.1.7)式有
地球物理数据处理教程
另外,设α1、α2为常数,δ函数对加法运算是线性的。
地球物理数据处理教程
对于任何在x0处连续的函数f(x),有
地球物理数据处理教程
上式称为δ函数的筛选性质。由于
地球物理数据处理教程
可知
地球物理数据处理教程
由于
地球物理数据处理教程
故有
δ(x)f(x)=δ(x)f(0)(8.1.14)
或同样
δ(x-x0)f(x)=δ(x-x0)f(x0)(8.1.15)
如果(8.1.14)式中取f(x)=x,得
xδ(x)=0(8.1.16)
若取f(x)在区间(-∞,α)(α为正数)外等于零,那么f(0)=0,于是
地球物理数据处理教程
由此推知
δ(x)=0x<0(8.1.17)
同理可得
δ(x)=0x>0(8.1.18)
这便是(8.1.2)式的由来。
两个δ函数的褶积由下式确定。
地球物理数据处理教程
于是
地球物理数据处理教程
下面我们给出δ函数的傅氏变换,根据δ函数的定义(8.1.1)式有
地球物理数据处理教程
反过来,数学上可以证明
地球物理数据处理教程
即是说δ(x)与1组成傅氏变换对,由(8.1.10)式设f(x)=cosωx,可得δ的余弦变换为
地球物理数据处理教程
标签:狄拉克,函数