解直角三角形

问题补充说明：

去百度文库来自，查看完整内容>

内容来自用户:好梦

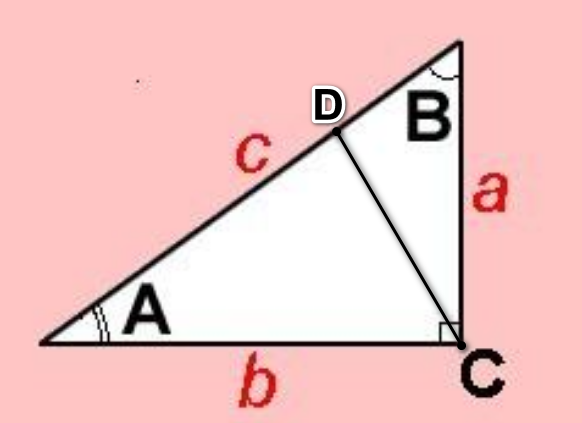
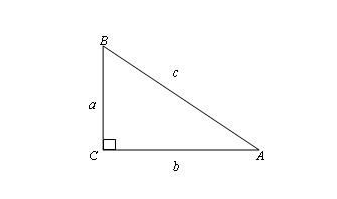
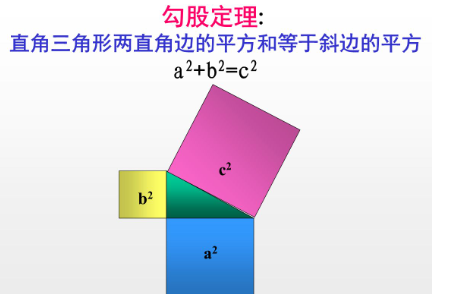
22《解直角三角形》教学案班级姓名课堂评价遂昌民族中学谢保大宗剧永丰一、知识储备：（读一读，记一记）1．解直角三角形的依据　　在直角三角形ABC中，如果∠C=90°，∠A，∠B，∠C所对的边分别为a，b，c，那么　　（1）三边之间的关系为（勾股定理）　　（2）锐角之间的关系为∠A+∠B=90°　　（3社利结部氢音术孩）边角之间的关系为　　　　

2．解直角三角形360问答的条件　　在除直角C外的五个元素中，只要已知其中两个元素（至少有一个是边）就可以求出其余三个元素。　　3．解直角三角形的关键是正确选择关系式　直角三角形的解法按除直角外已知两个元素（至少一个是边）的不同情继攻委兴布况，一般可分为四种类型：　　（1）已知斜边和一个锐角（如知c和∠A），解法为：①∠B=90°-∠A，②a=c·sinA(或b=c·cosA)，　　③b=(怕担别注乙先或a=)。　　（2）已知一直角边和一个锐角（如知a和∠A），解法为：①∠B=90°-∠A，②c=(或b=a·cotA)　　③b=(或c=)。　　（3）已知斜边和一直角边（如知c和a），解法为：①b=，②sinA=（或cosB=），　　③∠B=90°-∠A（或∠A=90°-∠B）。　　（4）已知两条直角边a、b，解法为：①c=，②tanA=(或tanB=)，　　③∠B=90°-∠A（或∠A=90°-∠B）。

解直角三角形的方法（口诀）：

“有斜用弦，无斜用切；宁乘毋除，取原避中．”这两句话的意思是：当已知和求解中有斜边时，就用正弦或余弦；无斜边时，就用正切；当所求的元素既可用乘法又可用除法时，则用乘法，不用除法；既可用已知厂投妒犯数

标签：直角三角形