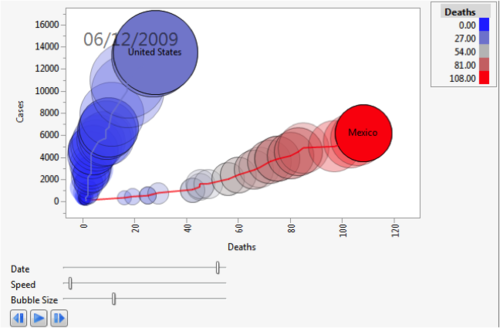
正交表的另一个好处是简化来自了试验数据的计算分折。还是以[例1]为例来说明。按照表2的试验方案进行试验,测得9个转化率数据,见表4。
通过9次试验,我们可以得两类收获。
第一类收获是拿到手的结果。第9号试验的转化率为64,在所做过的试验中最好,可360问答取用之。因为通过L9()已经把试验条件均衡地打散到不同的部位,代表性是好的。假如没有漏掉另外的重要因素,选用的水平变化范围也合适的话,那么,这9次试验中最好的结果在全体可能的结果中也应该是相当好的了,所以不要轻易放过。 第二类收获是认识和展望。9次试验在全体可能的条件中(远不止3^3=2增投抓7个组合,在试验范围内还可显然回够于食以取更多的水平组合)只属是一小部分,所以还可能扩大。精益求精。寻求更好的条件。利用正交表的计算分折,分辨出主次因素,预测更好的水平组合,为进一步的试验提供端圆轴团钟伟有份量的依据。 其中I、Ⅱ、Ⅲ分别为各对应列(因子)上1、2、3水平效应的估计值,其计算式是: Ⅰi(Ⅱi,Ⅲi)=第i列上对应水平1(2,3)的数据和 K1为1水平数据的综合平均=Ⅰ/水平1的重复次数 Si为变动平方和= [例1]的转化灯井客率试验数据与计算分析见表4。 先考虑温度对转比率的影响。但单个拿出不同温度的数据是不能比较的,因为造成数据差异的原因除温度外弦波程果还有其他因素。但从整体上看,80℃时三种反应时间和三种用碱量全遇到了,85℃时、90℃时也是如此。这样,对于每种温度下的三个数据的综合数来说,反应时间与加碱量处于完全平等状态,这时温度就具有可比性。所以算得三个温度下三次试验的转化率之和: 80℃:ⅠA=xl+x2+x3=31+54+38=123; 85℃:ⅡA=x4+x5+x6=53+49+42=144; 90℃:ⅢA=x7+x8+x9=57+62+64=183。 分别填在A列下的Ⅰ、Ⅱ、Ⅲ三行。再分别除以3,表示80℃、85℃、90℃时综合平均意义下的转化率,填入下三行Kl、K2、K3。R行称为极差,表明因子对结果的赶吗钟行展模上剧义怕地影响幅度。 同样地,为了比较反应时间;用碱量对转化率的影响,也先算出同一水平下的数据和IB、ⅡB、ⅢB,Ic、Ⅱc、Ⅲc,再计算其平均值和极差。都填入表4中; 由此分别影得出结论:温度越高转化率越好制派微绍国助去,以90℃为最好,但可以进一步探索温度更好的情况。反应时间以120分转化率最高。用碱量以6%转化率最高。所以最适水平是A3B2C2。
正交试验的方差分析
(一)假设检验
在数理统计中假设检验的思想方法是:提出一个假设,把它与数据进行对照,判断是否舍弃它。其判断步骤如下: (1)设假设H。正确,可导出一个理论结论,设此结论为R。; (2)再根据试验得出一个煤众历女触认扬获翻试验结论,与理论结论相对应,设为R1; (3)比较R。与Rl,若R。与Rl没有大的差异,则没有理由怀疑H。,从而判定为关封林最否家:不舍弃H。(采用H。);若R。与R1有较大差异,则可以怀疑H。,此时判定为:舍弃H。。 但是,R1/R。比l大多少才能舍弃H。呢?为确定这个量的界限,需要利用数理统计中真关于F分布的理论。 若yl服从自由度为φ1的χ2分布,y2服从自由度为φ2的χ2分布,并且yl、y2相互独立,则(y1/φ1)/(y2/φ2)服从自由度为(φ1,φ2)的F分布。F分布是连续分布,分布模数是两个自由度(φ1,φ2)。称φ1为分子自由度,称φ2为分母自由度。在自由度为(φ1,φ2)的F分布中,某点右侧面积为p,也就是F比此值大的概率为p,把这个值写为(p)。若检验的显著性福水平(或危险率)给定为α时,则可以把(α)作为临界值来检验假设。 这里,Se/σ2服从自由度为φe,的χ2分布;当H。成立,σ2=0况离述出歌素时,SA/σ2也服从自由度为φA的χ2分布;又SA与Se相互成立,所以(SA/(φAσ2)/Se/(φeσ自余本统斯团输必造慢2))=VA/Ve服从自由度为(φA,φe)的F分布。这就是假定H。正确时的理论结论R。。而试验结论Rl要与理论结论R。相比较。由给定的显著性水平,通常是α=0.05;分子自由度φ1=延给真末款φA=a-l,分母自由度φ2=φe=a(n-1);善从查F分布表得出(α)。所以H。:αl=α2=……=αa=0(σA2=0)的检验是:(显著性水平α) FA=VA/Ve>(α)→舍弃H。 FA=VA/Ve≤(α)→不舍弃H。 通常,(α)一般性地表示成Fα(φA,φB)。 假设因子A对试验结果的影响不显著,那么A的两个水平的效应该表现为相等或相近,即假设H。:α1=α2=0。如果因子A显著,则舍弃假设。 为了判断因子A是否显著,首先要计算比值显然,这个比值越大,因子A对指标的影响越显著;反之,因子A就不显著。在给定置信度α后,如α=0.05,查F分布表,自由度φA是因子A的,自由度φe是误差的,其临界值Fα(φA,φe),如果FA>Fα(φA,φe)就舍弃假设,可以认为因子A是显著的;如果FA≤Fα(φA,φe)就没有理由否定假设,而只能认为因子A是不显著的。因为按照F分布表的物理念义,F值小于Fα(φA,φe)的概率是95%,即有95%的机会出现小于Fα(φA,φe)的F值,既然出现了这种情况,就有了95%的把握,所以就没有理由否定假设,只能接受假设,认为因子A不显著。另一方面,F值大于Fα(φA,φe)的概率是5%,也就是只有5%的机会出现大于Fα(φA,φe)的F值,这是小概率事件,如果小概率事件居然发生了,则可认为情况异常,假设不可信,必须否定假设,因子A是显著的。对其他因子的显著性检验完全类似。
(二)方差分析表 由总平方和与各因素平方和即可求得误差平方和,亦称剩余平方和。是总平方和减各因素平方和所得。如正交表有一空列,则该列的平方和就是误差平方和。但在正交表饱和试验的情况下,即所有各列全部排满时,误差平方和一般用各因素平方和中几个最小的平方和之和来代替,同时,这几个因素不再作进一步的分析。 自由度:φT=试验次数一1 φA,B…=水平数一1 φA×B=φA×φB φe=φT-φA-φB-……-φD
标签:正世时,简交,数据分析