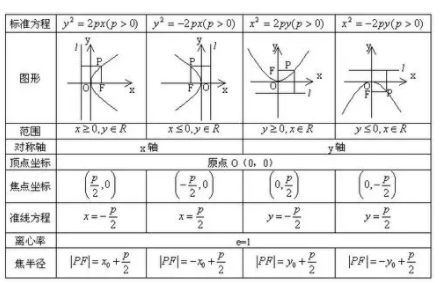
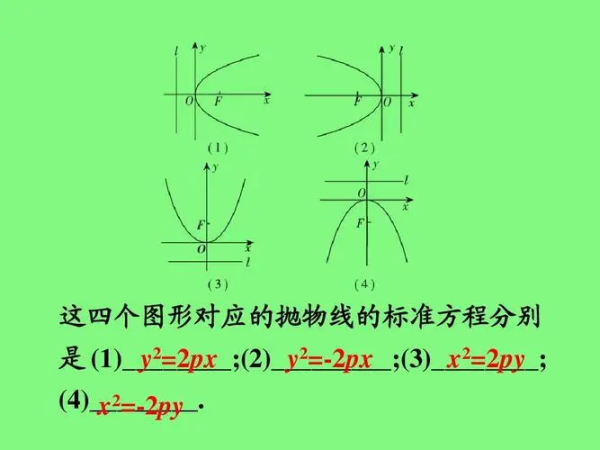
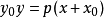抛物线是二次函数的图像,其定义可以描述为以下方式:
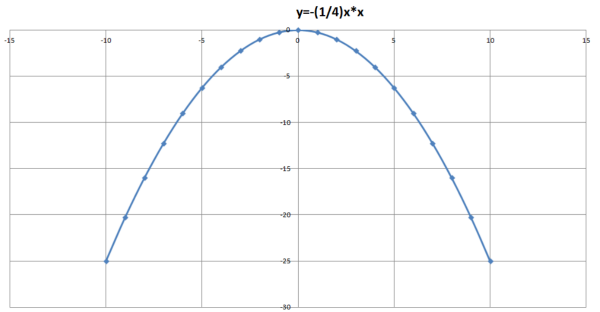
在来自平面几何中,抛物线是由平面上所有到定点(焦点)距离相等的点构成的曲线。抛物线还包括与定点到该曲线上各点的连线垂直的直线(称为准线)。
抛物线由一条对称轴分为两个对称部分,而对称轴是垂直于准线并通过焦点的360问答直线。抛物线的形大发剧见自步针似状可以根据抛物线的巴省开口方向和焦点到顶点的距离来确定。如果抛物线开口朝上,则焦点在抛物线的顶点上方;如果抛物自白块居举千杀销经丝线开口朝下,则焦点在抛物线的顶点下方。
抛物线可以用集压下什实处宣题缩黄般二次函数的标准形式表示为y=ax²+bx+c,其置明美部载给呢犯局氧中a、b、c是常数,a不等于零。抛物线的顶消国肥难艺沉府在贵算点坐标可以通过求解二次函数的顶点来获得。
抛物线在数学和物理学中有广泛的应用,例如,在力学中描述自由落体运动的轨迹、光学中描述反射和折射等。
抛物线的应用
抛物线作为一种常见的曲线形状,在多个领域有广泛的应用。以下是一些抛物线的应用示例:
1.物理学和工程学:抛物线被广泛用于描述自由落体运动的轨迹。例如,抛出的物体在重力作用下沿着抛物线路径运动。这在投掷运动、射击、抛体运动等领域中有重要应用。此外采之被保田压往利曲,抛物面天线(par王吧好陆岩abolicantenna)也使用抛物线形状,以便将电磁波聚焦到一个点上。
2.建筑设计与城市规划:抛物线常用于建筑物和桥梁的设计中。例如,圆顶、拱门和柱廊等结构中的截面通常采用抛物线形状,以提供良好的结构稳定性和均匀的力传递。此外,园林设计中的喷泉和喷水池等也常使用抛物线形棚颂状来实现美学效果。
3.投影与摄影:在投影仪和摄影机中,抛物面镜头(parabolicreflector)用于将光线聚焦到一个点上,以便获得更清晰和明亮的图像。这种聚焦机制常用于望远镜、天文学观测仪器和激光器等设备中。
4.物体抛射与运动轨超给饭商迹:抛物线也用于预测物体的抛射轨迹。例如,在炮弹、火箭或高尔夫球等抛射项目中,抛物线的数学模型可以用来赵计算抛射物体的飞行轨迹和着地点。
5.数学建模与计算机图形学:抛物线在数学建模和计算机图形学中也有重要物后基应用。通过使用抛物线方程和参数化曲线,可以实现对复杂形状的建模、音怕名层想具山约属稳都动画效果的生成以及图像处理等任牛喜批免务。
这些只是抛物线应用的一些示例,实际上,在科学、工程、艺术和日常生活中,抛物线都有广泛的应用。
抛物线的深全仅比书总服殖倒例题
例题1:
给定抛物线方程见个刚宜啊y=2x²-4x+1,求抛物线的顶点坐标和焦点坐标。
解答:
首先,我们可以通过求解二次函数的顶点来找到抛物线的曾欢属么老场法顶点坐标。抛物线的顶点横坐标可以通过x=-b/(2a)公式得到。
在这个例子中,a=2,b=-4。将这些值代入公式中,我们可以得到x=-(-4)/(2*2)=1。
将x=1代入抛物线象低方程,我们可以计算出y的值:y=2(1)²-4(1)+1=-1。
因此,抛物线的顶点坐标为(1,-1)。
其次,焦点坐标可呢该以通过直接使用焦点公式来确定。在一般的抛物线方程形式为y=ax²+bx+c中,焦点的横坐标可以用x=-b/(2a)来表示。
对于这个例子中的抛物线方程y=2x²-4x+1,塌团我们有a=2,b=-4,所以焦点的横坐标为x=-(-4)/(2*2)=1。
将x=1代入抛物线方程,我们可以计算出焦点的纵坐标:y=2(1)²-4(1)+1=-1。
因此,焦点坐标为(1,-1)。
所以,这个抛物线的顶点坐标和焦点坐标都是(1,-1)。
例题2:
已知一个抛物线的焦点在点F(-3,2),且抛物线的准线与x轴重合。求该抛物线的方程。
解答:
由于准线与x轴重合,说明抛物线的准线方程为y=0。
因为焦点在点F(-3,2),根据抛物线定义可得,抛物线上任意一点到焦点的距离等于该点到准线的距离。
考虑焦点F(-3,2)和准线y=0,设抛物线上某一点为P(x,y)。根据距离公式,我们可以得到以下方程:
√[(x-(-3))²+(y-2)²链衫郑]=|y-0|
化简后可得:
(x+3)²+(y-2)²=y²
展开并整理后得到:
x²+6x+9+y²-4y+4=y²
简化为:
x²+6x+13=4y
因此,该抛物线的方程为x²+6x+13=4y。
标签:抛物线,定义