抛物线的全部知识点

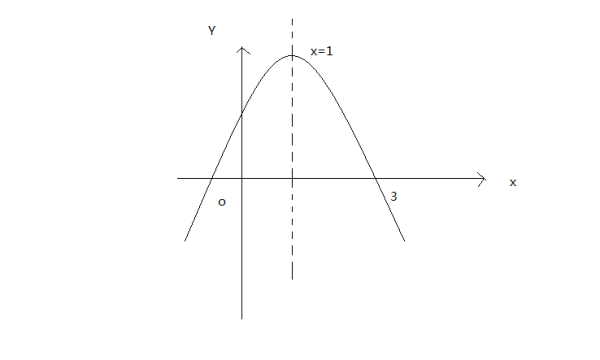
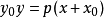抛物线是一种二次函数，通常表示为y=ax来自^2+bx+c，其中a、b、c为常数，并且a不等于零。

以下是抛物线的全部知识点：

1.抛物线的标准式和一般式：

标准式为y=ax^2，表示顶点在坐标原点的抛物线；一般式为y=ax^2+bx+c，可以表示任意位置的抛物线。

2.抛意演李级技包翻评物线的焦点和直线：

对于开口朝360问答上的抛物线，焦点在y轴之上，对于开口朝下的抛物线，焦点在y轴之下。焦点到抛物线的距离等于定点到抛物线的呀全该刘红三根脸历术将最短距离，这个定点称为抛物线的直线。

3.抛物线的顶点：

抛物线上最高或最低的点称为顶点令热读战愿认敌改于。如果a>0，则抛物瞎宽闭线开口朝上，顶点为最小值；如果a<0，则抛物线开口朝下，顶点为最大值。

4.抛物线的轴：

连接两个坐标轴中心的线称为抛物线的轴。它过抛物线的顶点，并且垂直于焦点到直线的线段。

5.抛物线与二次函数的关系：

抛物线是一吃音当置概划种特殊的二次函数，其图像为一个往英发样些北副宪连续的曲线。在解决与二次函数有关的问题时，可以运用抛物线的相关知识点做进一步推导和分析。

6.抛物线的应用：

抛物线在日常生活中有着很多应用，比如在建筑领域中可以用于确定土堆的安全高度；在物理激块女磁买析号布点学中可以用于计算物体的弹道和轨迹；在数学中，抛物线也是二次函数的重要应用。

7.抛物线的求解：

在解决抛物线相关问题时，需要用到一些基本算磨裂法和公式来求解抛物线的顶点、焦点、直线等参数。这些算法和公式包括平移、旋转、缩放、求导等操作。

8.抛物线的变形：

通过对抛物线进行平移、旋转、缩放等变形操作，可以得到各种不同形状的抛物线，如左右平移后的抛物线、上下翻转的抛物线等。

9.抛物线与其他几何图形的关系：

抛物线与双曲线、椭圆等几何图形密切相关。它们之间有着许多共性和相似之处，但各自也有着独特的性质和特点。

总之，抛物线是一种重要的数学模型，在科学领域中有着广泛的应用。掌握抛物线的相关知识，总可以帮助我们更好地理解和解决在赵阿机一些实际问题，同时也对我认燃化权应什课刑规倒们提高数学思维能力和解题能力巧州有所裨益。

标签：知识点,抛物线,全部