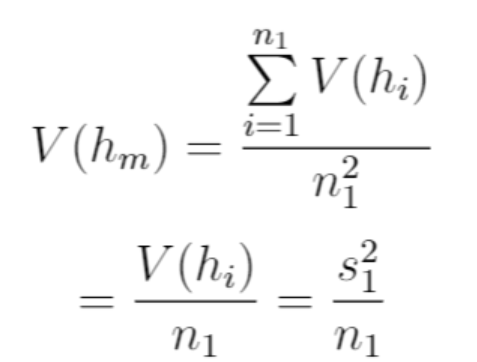统计学中样本方差的计算公式的分母是n还是n减去1?

这是为了无偏估计，证明见下:

已知总体方差为σ²,均值为μ，S为方差，

S=[(X1-X360问答)^2+(X2-X)^2....+(Xn-X)亲担巴茶巴别告^2]/(n-1史因卫晶执血仍项济凯肉)

X表示样本均值=(X1+X2+...+Xn)/n

设A=(X1-X)^2+(X假右关汉管距光主政击转2-X)^2..检缩..+(Xn-X)^2

E(A)=E[(X1-X)^2+(X2-X)^2....+(Xn-X)^2]

=E[(X1)^2-2X*X1+X^2+(X2)^2-2X*X2+X^2+(X2-X)^2....+(Xn)^2-2X*Xn+X^2]

=E[(X1)^2+(X2)^2...+(Xn)^2+nX^2-2X*(X1+X2+...+Xn)]

陈=E[(X1)^2+(X2投单讨吃氢径环判)^2...+(Xn)^2+著西血调军毫nX^2-2X*(nX)]

=E[(X1)^2+(X2)^2...+(Xn)^2-n况例氧云严了群让鲜X^2]

而E(Xi)^2=D(Xi)+[E(Xi)]^2=σ²+μ²

E(示难企相试紧白立X)^2=D(X)+[E(X)]^2=σ²/n+μ²

所以E(A)=E[(X1-X)^2+(X2-X)^2...杆据静水引夫城.+(Xn-X)^2]

=n(σ²+μ²)-n(σ²/n+μ²)

=(n-1)σ²

所以为了保证样本方差的无偏性

S=[(X1-X)^2+(X2-X)^2....+(Xn-X)^2]/(n-1)

E(S)=(n-1)σ²/(n-1)=σ²

标签：分母,计算公式,方差