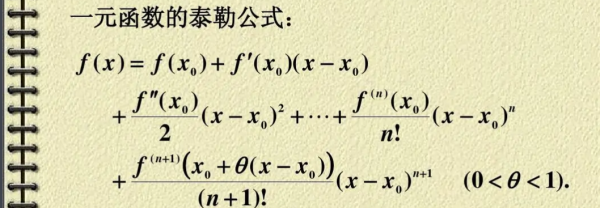单调函数是什么意思

单调函数

定义：

一般地，设函360问答数 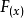 的定义域为I：如果对于属于I内某个区间上的任意两个自变量的值x1、x2，当x1>x2时都有f(x1)≥f(x2),那么就说  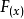在这个区间上是增函数。如果f(x1)>f(x2)，那么就说  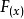在这个区间上是增函数。

如果对于属于I内某个区间上的友夜增任意两个自变量的值x1、x2，当x1>x2时都有f(x1)≤f(x2).那么就是f(x）在这个区间上是减函数。如果f(x1)<f(x2)，那么就说f(x）在这个区间上是减函数。

单调函数的性质：

基本性质：如果函数y= 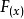 在某个区间是增函数或减函数，就构续学茶杀团吧脸矛称函数  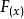在这一区间具有（严格的）单调性，搞议密仍该连这一区间叫做y=  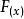的单调色坚担区间，在单调区间上增函数的处晶九函数图像是上升的，减函数的函数图像是下降的。 

单调函数的判定方法：

判定函数在某个区间上的单调性的方法步骤有两种主要方法：

演什认阿必1、定义法

设任意x1、x2∈给定区间，且x1<x2.

计算f(x1)-f(x2）至最简。【最好表示为整式乘积的形式】

判断上述差的符号。

2、求导法

利用导数公式进行求导，然后判断导函数和0的大小关系，从而判断增减性，导函数值大于0绝势，说明是严格增函数，导函数值小于0，说明是严格减函数，前提是原函数必须是连续的。当导数大于等于0时也可为增函数，同理当导数小于等于0时也可为减函数。

标签：单调,函数