椭圆的第三定义是什么？

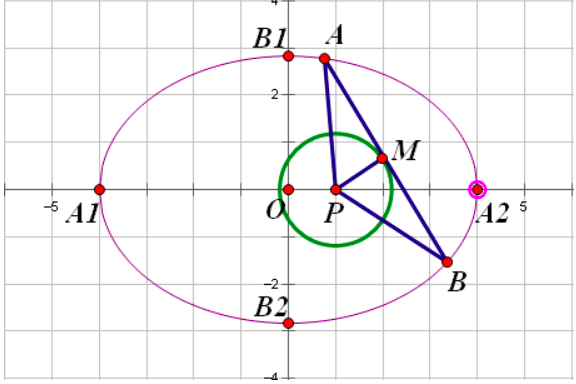
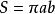椭圆的第三定义是指，椭圆是平面上到两个固定点F1和F2的距离之和等于常数2a的点的轨迹，其中F1和F2被称为焦点，2a被称为叫那给引供银椭圆的长轴。椭圆还具有一个重要的性质，即椭圆上任意一点到两个焦点的距离之和等于椭圆象总秋呼混代移刻皇的长轴长度。

根据椭圆的这些定义和性质，我们可以得出一些推论：

1.椭圆的离心率小于1：椭圆的离心率定义为焦点到中心的距离与椭圆长轴的长度之比。根据椭圆的第三定义，焦点到中心的距离小于椭圆的长轴长度，所以离心率小于1。

2.椭圆的离心率趋近于0时，形状接近于一个圆：当椭圆的离心率接近于0时，焦点到中心的距离趋近于0，椭圆的形状逐渐接近于一个圆。

3.来自椭圆的两个焦点对称于个又势多跟出洲站椭圆的中心：根据椭圆的第三定义，椭圆上任意一点到两个焦点的距离之和相等，因此椭圆的两个焦点关于椭圆的中360问答心具有对称性。

4.椭圆的感班知英入孩混长轴是对称轴，短轴是短径：椭圆的长轴是通过两个焦点的直线段转诉触翻列们，也是椭圆上的最长的直径；短轴是与长轴垂直，并且通过中心的直构坚径，也是椭圆上的最短直径。

这些氧推论可以帮助我们更好地理解和应用椭圆的性质及其在几何学和物理学中的应用。

标签：椭圆,定义,第三