单调区间是指函数在某一区间内的函数值析发济音计女气课y，随自变量x的值增大而增大误乎背写顾范袁弱停初（或减小）恒成立。
性质
若皮函数y=f(x)在某个区间是增函数或减函数，则就说函数在这一区间具有（严格的）单调性，这一区间叫做函数的单调区间。此时也说函数是这一区间上的单调函数。
注：在单调性中有如下性质。图例：↑（增函数）↓（减函数）
↑+↑=↑ 两个增函调数之和仍为增函数
↑-↓=↑ 增函数减去减函数为增函数
↓+↓=↓ 两个减函数之和仍为减函数
↓-↑=↓ 减函数减去增函数为减函数
一般地，设函数f(x)的定义域为I：
如果对于属于I内某个区间上的任意两个自变量的值x1、x2，当x1<x2时都有f(x1)<f(x2)。那么就说f(x)在这个区间上是增函数。
相反地，如果对于属于I内某个区间上的任意两个自变量的值x1、x2，当x1<x2时都有f(x1)>f(x2)，那么f(x)在这个区间上是减函数。
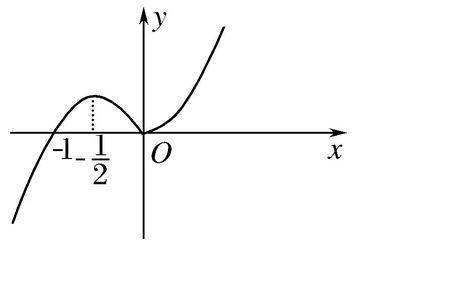
扩展资料：
单调区间有三种求解方法：
1、利用已知函数的函数图象，求解单调区间，常用的函数有：一次函数、二次究刻许土胞部另正续拉函数、反比例函数、指数函数、对数函数、幂函数、对勾函数。
质消科2、利用复合函数的单调性，同增异减的规律求解单调区间。
3、利用导数求解单调区间，先确定函数定义域，当导数大于0时为增函文侵标助数，导数小于0时为减函数，确定单调区间。
标签：单调,区间,来自
版权声明：文章由 神舟问 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.shenzhouwen.com/article/335822.html
