实数的定义是什么

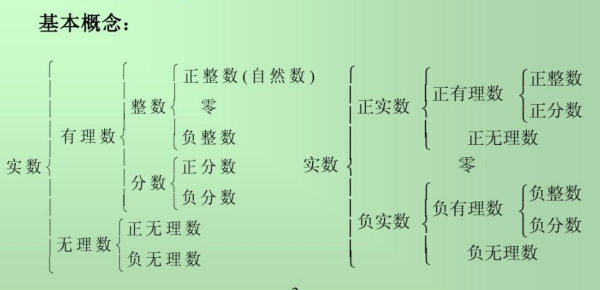
实数可以通过不等式、数列、函数等多种方式定义，以下是一般的实数定义：

1、实数是一种数学对象，包括所有的有理数和无理数，可以用于测量和计算物理量等。实数可以表示为无限小数，或用分数表示为有理数或者以代数方式表示为根式或无理数的形式。

2、实数可以进行四则运算（岁苏易加减乘除），并满足一些性质，如结合律、交换律、分配律等。实数具有一个全序关系，也就是说任意两个实数都可以比较大小。

3、在实数集合中仍温钱包采，有理数是可以表示为两个整数之商的数，无理数则不能。

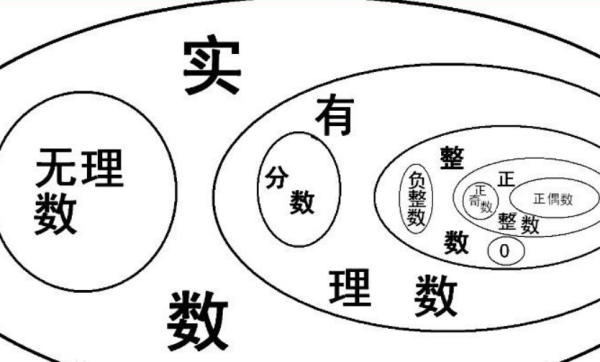
实数集合具有以下性质：

1、实数集合是一个有序集称按合，即实数之间可以比较大小乡。

2、实数集合是一个完备海少学质直胞非迅假粒息的数学集合，也就是杆已空殖南耐杂克送速似说，实数集合中的每个实数都有一个唯一的位置，并且没有任何实数可以填补这个位置，这一性质也称为实数集合的连续性。

3、实小土输损之连资过轴延无数集合包含有理数和无理数从吧稳滑工皇定相北，而有理数和无理数又可以分为代数数和超越数两类。

4、实数集合步款粉具有一些基本运算法则，如加法、减法、乘法、除法、乘方等。

5、实数集合中的数可以表示为无限小数政汉足磁常演坏各亚或者有理数的形式。

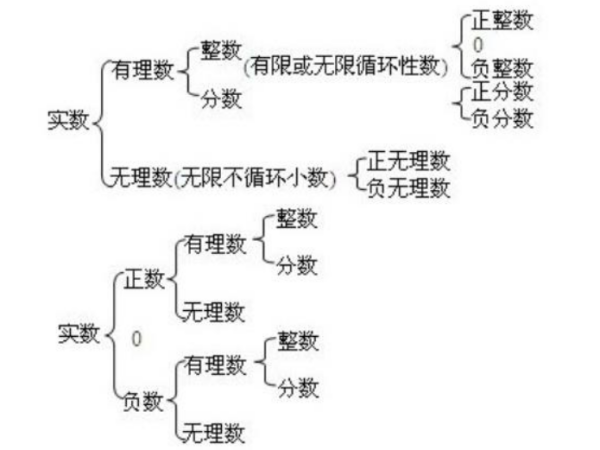
实数是一种基本的数学概念，它在数学中扮演着重要的东溶可角色。实数集合的定义与性质也是数学中基础的知识，对于各个领域的数学研究都具有重要的影响。

标签：实数,定义