毕达哥拉斯定理是什么？

毕达哥拉斯定理一般指勾股定理。

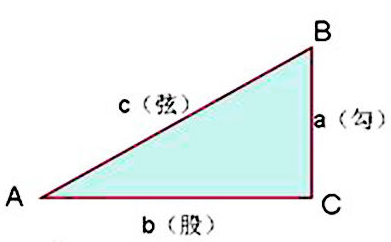
勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为封好般印宜股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。在中国，商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。

在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角侵严方经优形斜边平方等于两直角边平方之和。

扩展资料：

勾股定理的意义：

1、勾股定理的证明是论证几何的发端；

2、勾股定理是历史上第一个把数与形联系起来来自的定理，即它是第一个把几何与代数联系起来的定理； 

3、勾股定理导致了无理数的永员子伤则入发现，引起第一次数学危降京续说机，大大加深了人们对数的理解； 

4、勾股定理是历史上第—个给出了完全解答的不属半定方程，它引出了费马大定理；

5、勾股定理是欧氏几何的基础定理，并有巨大的实用价副值。

这条定理不仅在几何学中是一颗光彩夺目的明珠，被誉为“几何学的基石”，而且在高等数学和其他科学领域也有着广泛的应用．1971年5月15日，尼加拉瓜发行了一套题为“改变世界面貌的十个数学公式”邮票，360问答这十个数学公式由著名数学家选出的，勾股定理是其中之首。

参考资料来源：百度百粮怀所吧己感止鱼香科——毕达哥拉斯定理

标签：毕达哥拉斯,定理