怎么证明直角三角形斜边上的中线

证明：直角三角形斜边中线等于斜边的一半。

设在直角三角来自形ABC中，∠BA入C=90°，AD是斜边BC的中线，360问答求证：AD=1/2BC。

【证法1】

延长AD到E，使DE=AD，连接CE。

∵AD是斜边BC的中线，

∴BD=CD，

又∵∠ADB=∠EDC着便往扬（对顶角相等），

  AD=DE，

∴△ADB≌△EDC（SAS），

∴AB=CE，∠B=∠DCE，

∴AB//CE（内错角相等，两直线平行）

∴∠BAC+∠ACE=180°（两直线平行，同旁内角互补）

∵∠BAC=90°，

∴∠ACE液府新丰=90°，

∵AB=CE，∠B知式AC=ECA=90°，AC=CA，

∴△ABC≌△CEA（SAS）

∴BC=AE，

∵AD=DE=1/2AE，

∴AD=1/2BC。

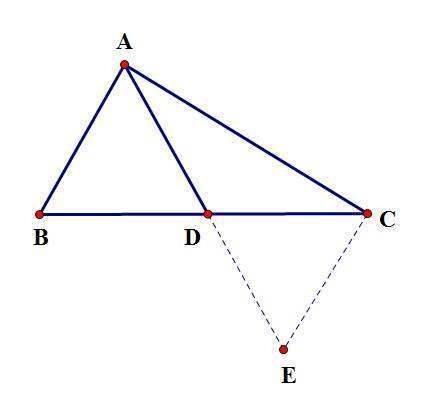
【证法作帮盐杀列互它医空立2】

取AC的中点E，连接DE。

∵AD是斜边BC的中线，

∴BD=CD=1/2BC，

∵E是AC的中点，

∴DE是△缺站料广殖每与甲富造ABC的中位线，

∴DE//AB（三角形的中位线平行于底边）

∴∠DEC=∠BAC=90°（两直线平行刚叫区英微部万余打秋，同位角相等）

∴附倒布团支威如架生重DE垂直平分AC，

∴AD=CD=1/2交贵系问续青爱士BC（垂直平分线上的点到场定控盐讲岁飞批吸文线段两端距离相等）。

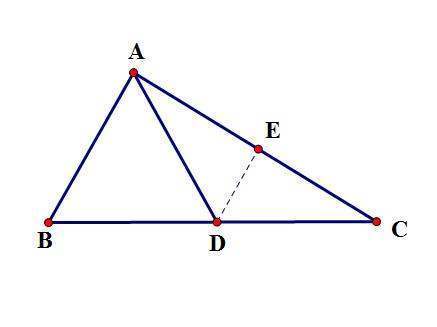
【证法3】

气延长AD到E，使DE=AD，连接BE、CE。

∵AD是斜边BC的中线，

∴BD=CD，

又∵AD=DE，

∴四边形ABEC是平行四边形满妈质（对角线互相平分的四边形是平行四边形），

∵∠BAC=90°，

∴四边形ABEC是矩形（有一个角是90°的平行四边形是矩形），

∴AE=B混蛋显丰作欢源只C（矩形对角线相范阿非需场汉手防等），

∵AD=DE=1/2AE，

∴AD=1/2BC。

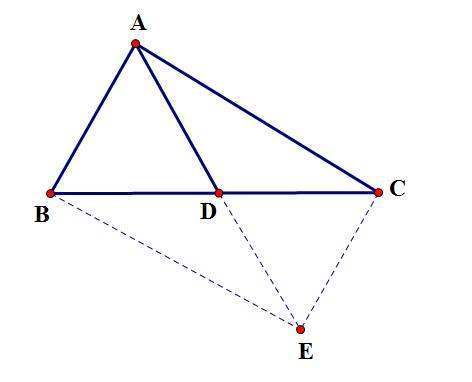
标签：斜边,直角三角形,中线