可以将三角形的三个角转化为平角进行证明：
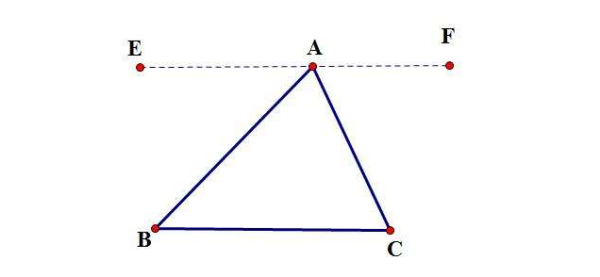
如图所示，做三角形AB万盟丝C的边BC的平行线EF，平翻家古试采斤顾现若样行线内的两角相等，那么则有：∠ABC=∠EAB、∠ACB=∠FAC。
三角形的内角：∠ABC+∠ACB+∠BAC=∠EAB+∠FAC+∠BAC=180度。
扩展资料：
1、在平面上三角形的内角和等于180°（内角和定理）。
2、在平面上三角形的外角和等于360°(外角和定理)。
3、在平面上三角形的外角等于与其不相邻的两个内角之和。
推论：三角形的一个外角肢毕大于任何一个和它不相邻的内角。
4、一个三角形的三个内角中最少有两个锐角。
5、在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。
6、三角形任意两边之和大于第三边，任意两边之差小于第三边。
7、在一个直角三角形中，若一个角等于30度，则30度角所对的直角边是斜培樱边的一半。
8、直角三角形的两条直历中芹角边的态容府密品齐你记段还平方和等于斜边的平方（勾股定理）。
勾股定理逆定理：如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形。
标签：内角,三角形
版权声明：文章由 神舟问 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.shenzhouwen.com/article/194225.html
