复合函数的单调性是什么？

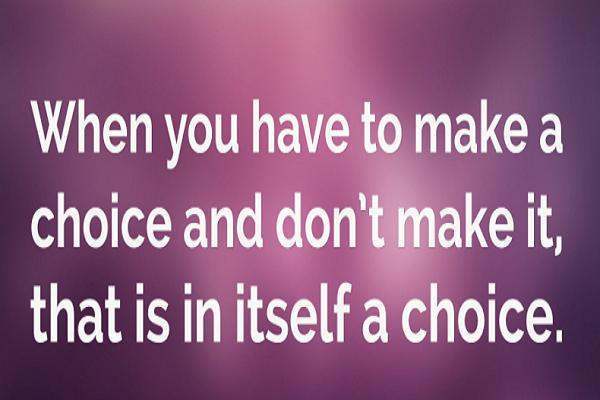
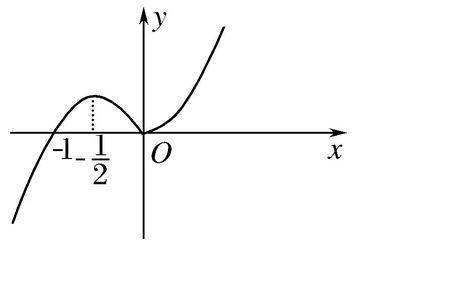
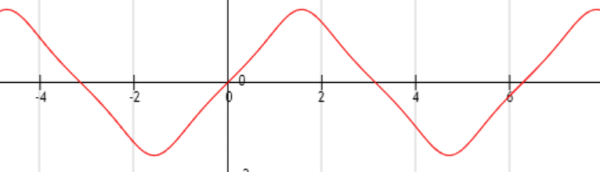
　复合函数的单调性一般是看函数包含的两个函数的单调性。

（1）如果两个都是增的，那么函数就来自是增函数。

（2）一个是减一360问答个是增，那就是减函数。

（3）两个都是减，那就是增函数。

设函数y=f(u)的定义域为Du，值域为Mu，函数u=g(x）的定义域为Dx，值域为Mx，如果Mx∩Du≠Ø，那么对于Mx∩Du内的任意一个x经过u；有唯一确定的y值与之对应，则变量x与y之间通过变量u形成的一权种函数关系，这种函数称为复体或径终班合函数(compositefunction)，记为：y=f[g(x)]，其中x称为自变量，u为中间变量，y为因变量（即函数）。

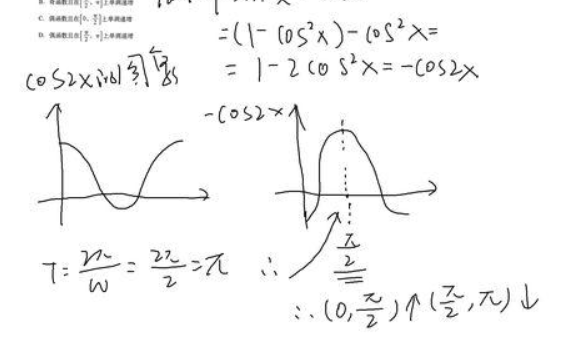
没扩展资料：

求函数的定义域主要应考虑以下几点：

⑴当为整式或奇次根式时，R的值域；

⑵当为偶次根式时，被开方数不小于0（即≥0）；

⑶当为分式时，分母不为0；当分母是偶次根式时，被表顶营流补各若开方数大于0；

⑷当为指数式时，对零指数幂或负整数指数幂，底不为0（如，中）。

⑸当是由一些基本函数通过四则运算结合而成的，它的定义域应是使轴应川将财解条素形层村各部分都有意义的自变量的值组成的集合，即求各部分定义域集合的交集。

标签：性是,单调,复合