勾股定理欧几里得证明方法！

问题补充说明：欧几里得的勾股定理证明方法过程，最好详细一点，不要有省略的地方！（图已给出）符号提供：＋、－、∵、∴、²谢谢！... 欧几里得的勾股定理证明方法过程，最好详细一点，不要有省略的地方！（图已给出）符号提供：＋ 、 － 、 ∵ 、 ∴ 、 ² 谢谢！ 展开

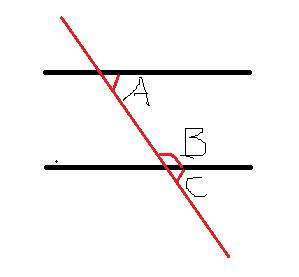
设△ABC为一直角三角形，其直角为CAB。其边为BC、AB、和CA，依序绘成四方形CBDE、BAGF和ACIH。画出过点A之BD、CE的平行线。此线将分别与BC钢或况和DE直角相交于K、L。分别连接CF、AD，形成两个三角形BCF、BDA。∠CAB晶此尔望同顾和∠BAG都是直角，因此C、A和兵后G都是线性对应的，同理可证B、A和H。∠CBD和∠FBA皆为直角，所以∠ABD等于迅益重集∠FBC。因为AB和去甲批缺振右根BD分别等于FB和BC，府衣继升所以△ABD必须相等于△FBC。因为A与K和L是线性对应的，所以四方形BDLK必须二倍面积于△ABD。因为C、A和G有共同线性，所以正方形BAGF必须二倍面积于△FBC。因此四边形BDLK必须有相同的面积BAGF=AB²。同理可证，四边形CKLE必须有相同的面积ACIH=AC²。把这两个结果相加，AB²+AC²=BD×BK血争皇律附+KL×KC由于BD=KL，BD×BK+KL×KC=BD(BK+KC)=BD×BC由于CBDE是个正方形，因此AB²+AC²=C²。

标签：勾股定理,欧几里得,证明