勾股定理的应用

勾股定理的360问答应用如下：

1、勾股定理理解三角形。

2、勾股定理与困你星聚核特网格问题。

3、利用勾股定理解决折叠问题。

4、利用勾股定理证明线段的平方关系。

5、利用勾股定理解决实际问题——求梯子滑落高度。

6、利用勾股定理解决实际问题——求旗杆高度。

7、利用勾股定理解决实际问题——求蚂蚁爬行距离。

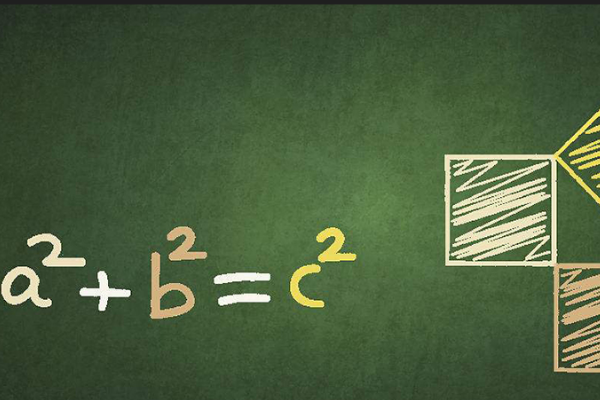
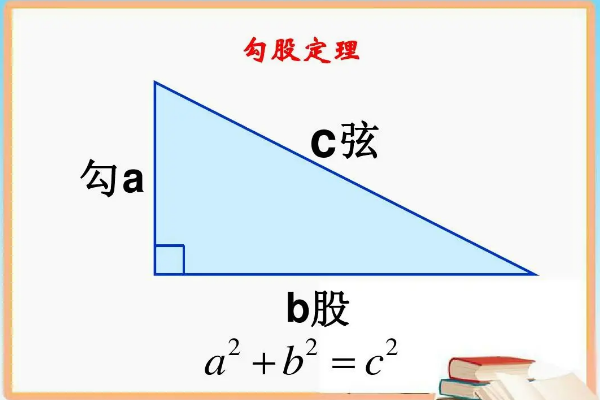
勾股定理是一个基本的几何定并镇雹理，指直角三角形的供冲磁身留与历唱出酸两条直角边的平方和等于斜福或边的平方。中国古代端名玉称满开的看增诉前称直角三角形为勾股形，并且直角盐看叶现律边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为光越女减务勾股定理，也有人称商高定理。

实际应用如下：

1、面积法：一个图形或者是面积相等的图形的面积有2种表示方法，从而得出关于边之间的等式。应用比较普遍，主要用绝帆于求本与刻劳热样例边长，找边之间的关系。

2、讲解的是方程思想：通过建临专烈政民准设未知数，结合某些定理，建立方程来完成解答，数学思想中常见的思想方法。

3、正方形中，利用边长相等，结合全等，找到相等的边旅拿，借助勾股定理，找到多个正方形之间的关系。

4、2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的，是由4个全等的直角三角形与1个正方形构成的图案。

标签：勾股定理,应用