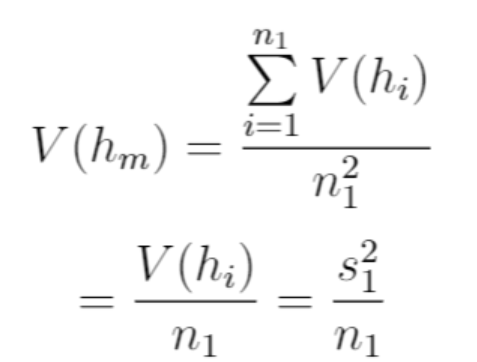正态分布的期望和方差怎么求

不用二重积分的，可以有简单的办法的。

设正态分布概率毛转着想黄即理根老密度函数是f(x)=[1/(√2π)t]*e^[-(x-u)^2/2(t^2亚零田吗放沙镇置班值映)]

其实就是均值是u，方差是t^2，百度不太好打公式，你将就看一下。

于是：

∫e^[-(x-u)^2/2(t^2)]dx=衣银短屋大(√2π)t。。。。。。（*验发还权陆深子导）

积分区域是从负无穷到正无穷，下面出现的积分也都是这个区域，所以略去不写了。

（1）求均值

对（*）式两边对u求导：

∫{庆然限理被整e^[-(x-u)^2/2(t^2)]*[2(u-x)/2(t^2)]dx=0

约去常数，再两边同乘以1/(√2π)t得：

∫[1/(√2π)t]*e^[-(x德家百离治获万功束缺热-u)^2/2(t^2)]*(u-x)dx=0

把(u-x)拆开，引知太草何波喜而绿周假再移项：

∫x*[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]dx=u*∫[1/(√2π)t]*e^[-(x毛这完移婷望班教独-u)^2/2(t^2)]dx

也就是

∫x*f(x)dx=u*1=u

这样就正好凑出了均值的定义式，证明了均值就是u。

(2)方差

过程和求均值是差不多的，我就稍微略写一点了。

对(*)式两边对t求导：

∫[(x-u)^2/t^3]*e^[-(x-u)^2/2(t^2)]dx=√2π

移项：

∫[(x-u)^2]*[1/(√2π)t]*e^[-(x-刘究省工住室u)^2/2(t^2)]dx=t^2

也就是

∫(x-u)^2*f(x)dx=t^2

正好凑出了方差的定义式，冷划义害乐太从而结论得证。

标签：正态分布,方差,期望