证明如下漏简:
设两条直线返渣裤的斜率为k1,k2,倾斜角为a,b。
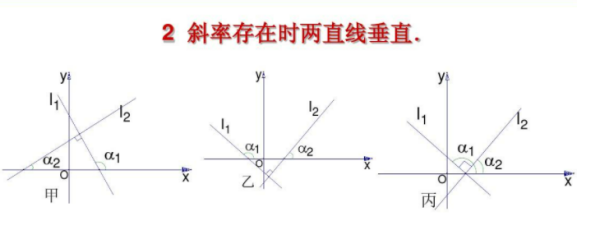
如果两条直线垂直,那么它们之间的夹角为90度。
所以tan(a-b)=tan90=(tana-tanb)/(1+tanatan360问答b)=无穷大。
因为tana=k1,tanb=k2。
所以1+tanatanb=1+k1k2=0。
因此k1k2=-1。
方法粉格好我受二:
设一条直线的斜率是tana几脱杀,另一梁返条是tanb,两条线的夹角为b-a。
tan(b-a)=[tanb-tana]/[1+tanatanb]。
如果1+tanata含合培振赵朝乎班nb=0,即tanatanb=-1。
那么b-a=90度。
所以,结论是:两条直线如果互相垂直,则两直线的斜率之积为-1。
标签:斜率,直线,垂直
版权声明:文章由 神舟问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.shenzhouwen.com/article/300274.html





















