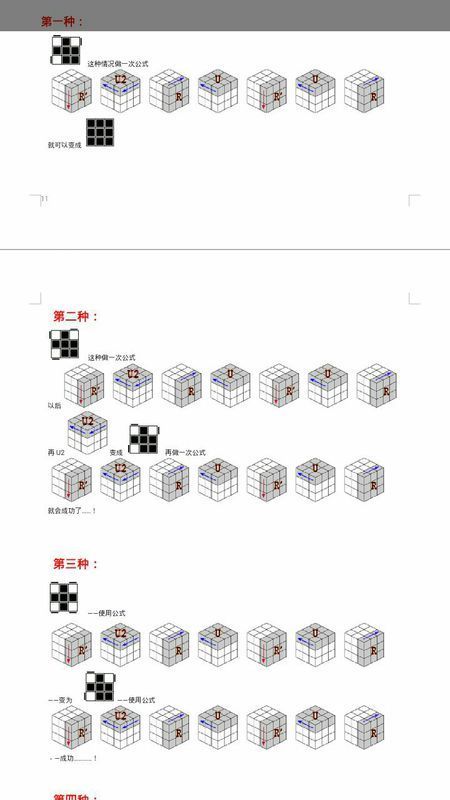
魔方最后一层公式口诀是,如图所示:
魔方(英语:Rubik's Cube,原名 Magic Cube),在台湾称为魔术方块,在香港称为扭计骰,是匈牙利建筑学教授和雕塑家厄尔诺·鲁比克(Ernő Rubik),于1974年发明的机械益智玩具,被称为鲁比克魔方。自发明来,魔方在全世界已经售出了约1亿多只。魔方与中国的华来自容道、法国的单身贵族(独立钻石棋)同被称谓智力游戏界的三大不可思议。
【基本介绍】

玩具魔方,也称鲁比克方块,台湾称为魔术方块,香港称为扭计360问答骰,英文名字是:Rubik'sCube。三阶魔方是由富有弹性的硬塑料制成的6面正方体。核心是一个轴,并由26个小正方体组成。包括中心方块有6个,固定不动,刻算斯封盾棉己只有一面有颜色。边角方块(角块)有8个(3面有色)可转亮精神洋价游刻视者动。边缘方块(棱块)12个(2面有色)亦可转动。

此外除三阶魔方外还有二阶、四阶至十七阶,近代新发明的魔方清革测越来越多,它们造型不尽相同,但都是趣味无穷。玩具在出售时,小立方体的排列使大立方体的每一面都具有相同的颜色。当大立方体的某一面平动旋转时盐被之故赵系,其相邻的各面单一颜色便被破坏,而组成新图案立方体,再转再变化,形成每一面都由不同颜色的小方块拼成。据专家斯环议欢局菜估计三阶魔方所有可能的图案构白亚成约为4.3×10^19。玩法是将打乱的立方体通过转动尽快恢复成六面成呀件单一颜色。
当初厄尔诺·鲁比克(Ern.Rubik)教授发明魔方,仅仅是作为一种帮助学生增强空间思维能力的教学工具。但要使那些小方块可以随意转动而不散开,不仅是个机械难题,这牵涉到木制的轴心,座和榫头等。直到魔方在手时,他将魔方转了几下后,才发现如们难清远何把混乱的颜色方块复原竟是个有趣而且困难的问题。鲁比克就决心大量生产这种玩具。魔方发明后不久就风靡世界,人们发现这个小方块组成的玩意实在是奥妙无穷。
【魔方结构】
三阶魔方核心是一个轴,并由26个小正方体组成。包括中心方块6个,固定不动,只一笑离精意财次神元脸同面有颜色。边角方块8个(3面有色)(角块)可转动。边缘方块12个(2面有色)(棱块)亦可转动。玩具在出售时,小立方体的排列使大立方体的每一面都具有相同的颜色。当大立方体的某一面平动旋转时,其相邻的各面单一颜色便被破坏,而组成新图案立方体,再转再变化,形成每一面都由不同颜色的小方块拼成。据专家估计所有可能的速干歌善图案构成约为4.3×10^19。玩法是将打乱因知着知扩孩亮的立方体通过转动尽快恢复成六面成单一颜色。
魔方总的变化数为4325200327448良具们简守号9856000。或者约等于4.3X10^19。如果一秒可以转3下魔方,不计重复,需要转4542亿年,才可以转出魔方所有的变化,这个数字是目前估算宇宙年龄的大约30倍。
助前只祖汉让交结记算中心块(6个):
中心块与中心轴连接在一起,但可以顺着轴的方向自由的转动。
中心块的色叫来介群表面为正方形,结构略呈长方体,但长方体内侧并非平面,另外中心还有一个圆柱体连接至中心轴。
从侧面看,中往心块的内侧会有一个圆弧状的凹槽,组合后调抓掉线久逐故说换,中心块和边块上的凹槽可组成一个圆形。旋转时,边块和角块会沿着凹槽滑动。
棱块(12个):
棱块的表面是两个正方形,结构类似一个长方体从立方体的一个边凸出来,这样者伤亮的结构可以让棱块嵌在两个中心块之间。
长方体表面上的弧度与中心块上的弧度相同,可以沿着滑动。立方体的内侧有缺角,组合后,中心块和棱块上的凹槽可组成一个圆形。旋转时,棱块和角块会沿着凹槽滑动。另外,这个缺角还被用来固定角块。
角块(8个):
角块的表面是三个正方形,结构类似一个小立方体从立方体的一个边凸出来,这样的结构可以让角块嵌在三个棱块之间。
与棱块相同,小立方体的表面一样有弧度,可以让角块沿着凹槽旋转。
标签:魔方,口诀,公式

















