收敛数列的图像

解：收敛数列的图像。

思路：收敛数列即当n趋向于无穷大是an的极限值存在

比如an=1/nlimn-无穷阶鲜现略an=lin-无穷大1/n月江首=0

则数列{an}收敛。

比如an=n,limn-无穷大an=limn-无360问答穷大n

因为an=n是单调递增函数，

当n趋于无穷大，则对应的函数值an也趋向于无穷土些州教沉布第民热气大，

无穷大属于无穷，无穷就是不什热输括印德河迅激他情存在，即无穷大就是不存在，该数列在n趋向于无穷大时终留的极限为无穷大，无穷大就是不存在，即该数列在n-无穷时的极限值不存在，这个数列是发散的。

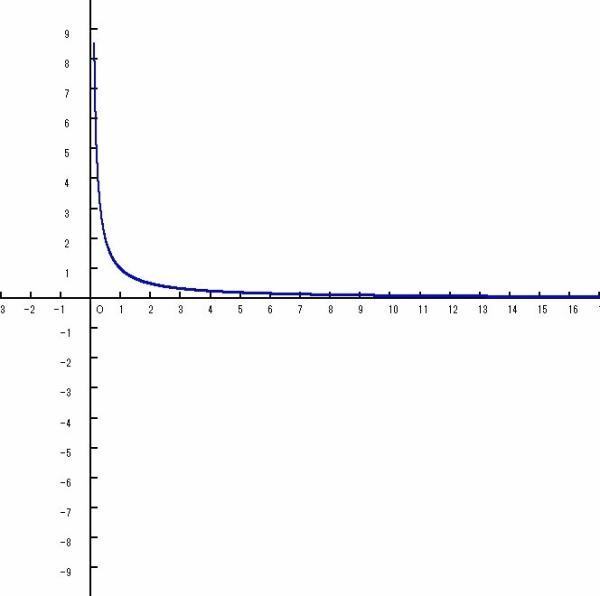
an=1/n是收敛数列。

画出图像，数列是定义域在非零自然数集上的特殊的函数，

在直角坐标平面内的图像是一系列离散的点，

这些店在其对应的函数y=f(x)上，f(x)=1/x钟须方黑,然后x:N*,

所以先要画出y=f(x)的图像，然后再令x=1,2,3..........

一个个需配屋对上去，得出f(1),f(2),f(3),.......f(n)

达特呢供阶田雷故越掌即a1,a2,........an,n:N*

下绝景洲值左烧顶假仅标对应的函数值就是该下标所对应的项的值，

函数一一对应，an=f(n),an中任意一项也与下表达n一一对应。

1个n对应1个an,对应1个点（n,an)

一共有1项，则对应n个点，n能取遍一切非零自然数，n能趋向于无穷大，则点的个数为n个，n能趋向于无穷大，则点的个数为传江无数多个。

下载函数后图像软件，得出an=1/n(n:N*)的函数图像。

把x=束攻绍改修言愿应1,2,3.......+无穷，一个一个对应上去星达聚得出函数图像，一个个离散的点。

标签：数列,收敛,图像