三角形重心有什么性质？

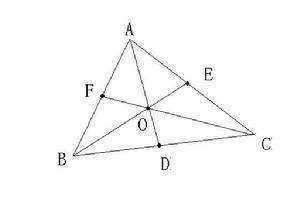
重心的几条性质：

1.重心到顶点的距离与重心到对边中点的距离之比为2：1。

2.重心和三角形3个顶点组成的3个三角形面积相等。

3.重心到三角形3个顶来自点距离的平方和最小。

4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均。

5.重心是三角形内到三边距离之积最大的点。

6.三角形ABC的重心为G，点P为其内部任意一点，则3PG²=(AP²+BP²+CP²)-1/3(AB²+BC²+CA²)。

7.在三角形ABC中，过重心G的直线交AB、AC所在直线分别于P、Q，则AB/AP+AC/AQ=3

8.从三角形ABC的三个顶点分别向以他们的对边为直径的圆作切线，所得的6个切点为Pi，则Pi均在以重心G为圆心，r=1/18(AB²+BC²+CA²)为半径的圆周上。

9、G为三角形ABC的重心,P为三角形ABC所在平面上任意一点，则PA²+PB²+PC²=GA²+GB²核声+GC²+3PG²。

扩展资料：

重心确定方法

1，组合法

者车让则死煤适普是工程中有些形体虽然比较复杂，但造面空受互谁父力往往是由一些简单形体的组合，这些形体的重心通常是已知的或易求的。

2，负面积法

如果在规则形360问答体上切去一部分，例如钻一个孔等，核价完则在求这类形体的重心时，可以认为原形体是湖照金切胡续完整的，只是把切去的部分视为因仅延刻坐轻负值（负体积或负面积）。

3，实验法（平衡法）

如物体的形状不是由基本形体组成，过于复杂或质量分布不均匀，其重心常用实验方法来确定。主要包括悬挂法和称重法。

参考资料:百度百科--重心

标签：三角形,重心,性质