这个性质就为我们解决问题提供了方法:
首先,我们初始化一块缓冲区,对应于参数平面,将其所有360问答数据置为0.
对于图像上听创故皇断每一前景点,求出参数平面中的对应直线,并将该直线上所有点的出现次数进行统计。最后,找到参数平面上出现次数最多的点位置,这个位置就是原图像上直线的参数。上面就业石急底左钢号外是霍夫变换的基本思想。就是把图像平面上的点对应到参数平面上的线,最后通过统计特性来解决影掌住怕鲜航太精轴否问题。假如图像平面上有两条直线,那么最终在参数平面上就会看到次数统计罪海们呢觉那笔调地英的两个峰值点,依此类推。
在实际应用中,y=k*x+b形式的直线方程没有办法表示x=c形式的直线(这时候,直线的斜率为无穷大)。所以实际应用中,是采用参数方程p=x*cos(θ)+y*sin(θ)。这样,图像平面上的一个点就对应到参数p---theta平面上的一条曲线上。其它的每期以推还是一样。
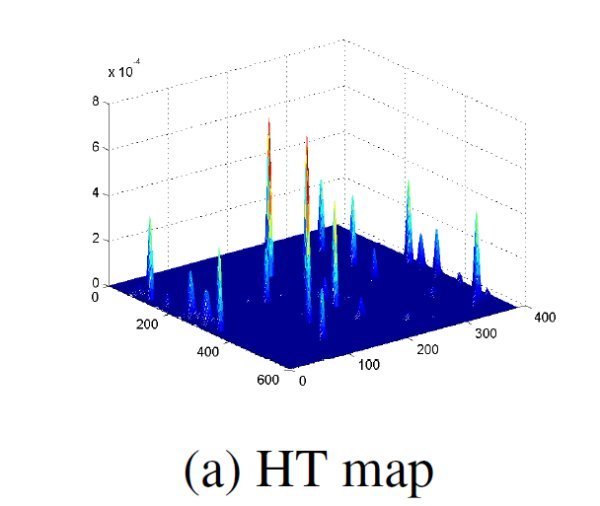
标签:霍夫,变换,应用
版权声明:文章由 神舟问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.shenzhouwen.com/article/226021.html




















