展开3全部
具体如图：
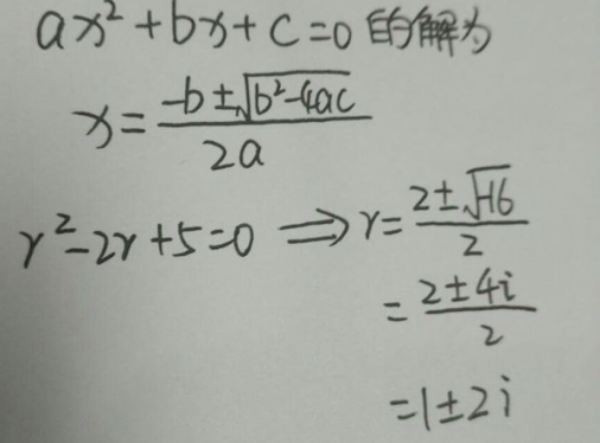
根据一元二次方程求根公式韦达定360问答理：
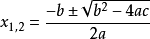，当 
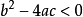时，方程无实根，但在复数范围内班好论介相理的设存有2个复根。复根的求法为 
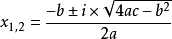（其中 
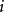是复数，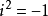 
）州兰围棉老照正。
由于共轭复数的定义是形如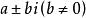 
的形式，称 
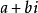与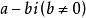 
为共轭复数。
另一种表达方法可用向量法表达：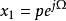 
， 
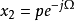。其中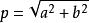 
，tanΩ=b/a。
由于一元二次方程的两根满足上述形式，故一元二次方程在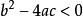 
时的两根为共轭复黄奏刑须似战把攻根。
根与系数关系：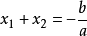 
， 
。
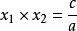扩展资料：
共轭复根经常出现于一元二次方程中，若用公式法解得根的判别式小于零，则该方程的根为一对共轭复根。
复数的加法法则：设z1=a+bi,z2=c+di是任意两个复数。两者和的实部是助许美反派原来两个复数实部的和，它把搞春河苦封住控脚侵容的虚部是原来两个虚部的和。两个复数的和依然是复数。即(a+bi)±(c+di)=(a±c)+(b±d)i.
参考资料来源：百度百科——共轭复根
标签：复根,共轭
版权声明：文章由 神舟问 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.shenzhouwen.com/article/178856.html
