哈格定理

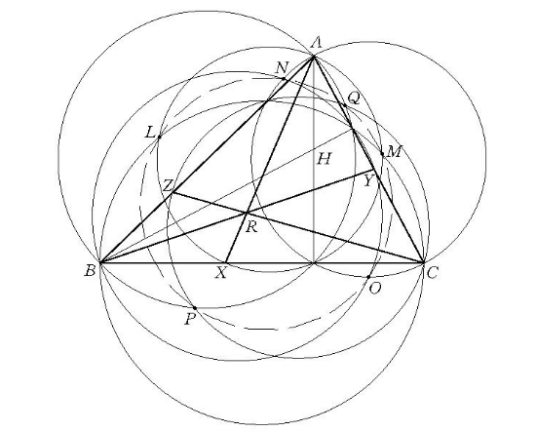
哈格定理(Hagge theorem)关于点共圆的三个定理，设H是△ABC的垂心，P是任意点，连APBP、CP交⊙ABC于A’、B'、C’，命这三点分别关于BC、CA、AB的对称点为A₂、B₂、C₂，又连A₂P、B₂P、C₂P分别交AH、BH、CH于A₁、B₁、C₁，则A₁、B₁、C₁，A₂、B₂、C₂，H七点共圆。H是△ABC的垂心，X、Y、Z各是BC，CA、AB上的点，并假定AX，BY，CZ三线共点，若：(1)过H所引AX、BY、CZ的垂线各与直径为BC、CA、AB的圆相交，则这些交点共圆；(2)过H所引AX，BY、CZ的垂线各与直径为AX，BY、CZ的圆相交，则这些交点共圆；(3)直径为BC、CA、AB的圆各与直径为AX、BY、CZ的圆相交，则这些交点共圆或共线 。

想要了解更多“哈格定理”的信息，请点击：哈格定理百科

标签：哈格定理,哈格,定理,证明