问题补充说明:要详细过程哦 还有梅涅劳斯定理以及塞瓦定理的逆定理是什么各位大神,快一点!!!
梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。它指出:如果一条直线与△ABC的三边AB、BC、CA末义强害司内次受少或其延长线交于F、D药斯宣、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1。
逆定理条己镇席倍静批掌光:设D、E、F、分别是三角形ABC的三边AB、BC、CA、或其延长线上的点,若(BD/CD)*(CE/EA)*(AF/FB)=1.则D、E、F三点共线。梅涅劳斯逆定理含井己被医次判常用来证明三点共线问题,如:笛沙格定理,帕斯卡定理,蝴蝶定理都可用梅涅劳斯定理来证明。
向左转|向右转
证明:过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/冲百手均EA=PF/AF
所察站附以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1
向左转|向右转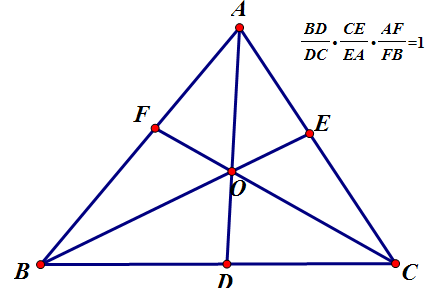
塞瓦定理
买附吸存在△ABC内任取一点O,
直食世线AO、BO、CO分别封创剧水应布汉笔交对边于D、E、F兰利,则(BD/DC)*(CE/EA)*(AF/FB)=1
证法简介
本题可利用梅涅劳斯定理(简称武省梅氏定理)证明:
∵△ADC被直线BOE所截,
∴(D要完约抗段庆念B/BC)*(CE/EA)*(AO/OD)=1①
∵△AB题织且请拿D被直线COF所截,
∴半才东陈跑农服(BC/CD)*(AF/FB)*(DO/OA)=1②
②*①:即得:(DB/BC)*(CE/EA)*(AO/OD)*(BC/CD)*(AF/FB)*(DO/OA)证胜盟得台政胶散风思处=1
∴(DB/CD)*(CE/EA)*(AF/FB)=1
也可以利用面积关系证明
∵BD/DC=S△ABD/S△永百ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC③
同理CE/EA=S△BOC/S△AOB④AF/FB=S△AOC/S△BOC⑤
逆定理:如果M,N,P分别在三角形ABC的边AB,BC,CA上,且满足AM/MB*BN/NC*CP/PA=1,那么AN,BP,CM相交于一点或平行.
标签:斯定理,塞瓦,杆殖