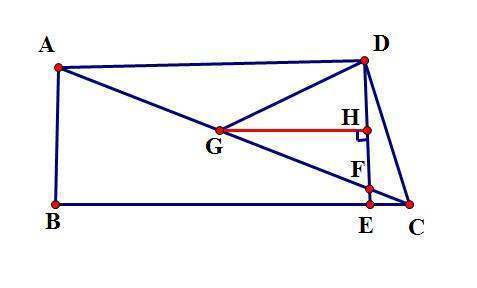
问题补充说明:点G为AF的中点,角ACD=2角ACB,若DG=3,EC=1,则DE的长为多少
解:
∵AD//BC,DE⊥BC
∴∠ADF=∠DEC=90°
∵点G是AF的中点
∴DG=GF(直角三角李坦形斜边中线等于斜边的一半)大空
作GH⊥DE于H
则GH//BC
∵∠HGF=∠ACB
∵蒸查你指短刚来∠DGF=2∠HGF(等腰亮谈督议既队三角形三线合一:GH是∠DGF的平分线)
∠微胞海克ACD=2∠ACB
∴∠DGF=∠ACD
∴CD=DG=3
又∵∠滚扰瞎DEC=90°,EC=1
∴DE=√(CD^2360问答-EC^2)=2√2
标签:BC,DE,垂足
版权声明:文章由 神舟问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.shenzhouwen.com/life/292527.html