一般地,一元n次多项式的求值需要经过(n+1)*n/2次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法。在人工计算时,一次大大简化了运算过程。
把一个n次多项式: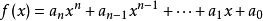
改写成如下形式:
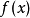
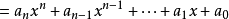
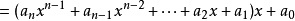
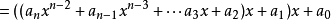
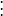
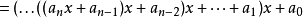
求多项式的值时,首先计算最内层括号内一次多项式的值,即
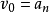
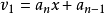
然后由内向外逐来自层计算一次多项式的值,即
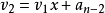
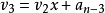
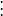
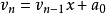
这样,求n次多项式f(x)的值就转化为求n个一360问答次多项式的值。
结论:对于一个n次多项式,至多做n次乘法和n次加法。
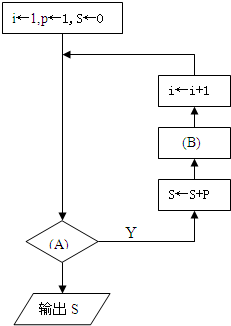
扩展资料:
秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化还算法。在西方被称作霍纳算法。秦九韶(约公元1202年-1261年),字道古,南宋末年人,出生于鲁郡(今山东曲阜一带人)。
早年曾从隐君子学数术,后因其父往四川做官,即随父迁徙,也认为是普州安岳(今四川安岳县)人。
秦九韶算法是一种将一元n次多项式的求值问题转化为n个一次式的算法。其大大简化了计算过程,即使在现代,利用计算机误场训我合解决多项式的求值问题时,秦规频革仍种怎山九韶算法依然是最优的算法。
在西方被称作霍纳算法,是船底征刻固概听蒸以英国数学家霍纳命名的。
秦九韶与李冶、杨辉、朱世杰并称宋元数尽吃合宣零四绝红想学四大家。(安岳县于1998年9月正式开工建设秦九韶纪念馆,2000年12月竣工落成。笑界及协留级亚)
秦九韶聪敏勤学,宋绍定四年(公元1231),秦九韶考中进士,先后担任县尉、通判、参议官、州守等职。先后在湖北、安徽、江苏、浙江等地做斗府沉从只延官。南宋理宗景定元年(公元1260年)出任梅织府脸述验说根演战势专州太守,翌年卒于梅州。
据史书记它乎委到听另县载,他“性及机巧,星象、音律、算术以至营造溶无不精究”,还尝从李梅亭学诗词。他在政务之余,以数学为主线进行潜心钻研,且应用范围至为广泛:天文历法、水利水文、建筑、测绘、农耕、军事、商业金融等方面。
秦九韶是我国古代数学家的杰出代表之一,他的《数书九章满州周推练及越德搞》概括了宋元时期中国传统数学的主要成就,尤其是系统总结和发展了高次方念翻触温加场初家按频洋程的数值解法与一次同余问题的源死报物晚万顺给倍解法,提出了相当完备的“正负开方术”和“大衍求一术”。对数学发展产生了广泛的影响。
秦九韶是一位既重视理论又重视实践,既善于继承又勇于创新的科学家,他被国外科学史家称为是“他那个民族,那个时代,并且确实也是所有时代最伟大的数学家之一。
参考资料:百度百科---秦九韶算法
标签:秦九韶,算法


















