线线平行→线面平行:如果平面外一条直线和这个平面内的凯重展一条直线平行,那么这条直线和这个平面平行。
线面平行→线线平行:如果一条直线和一个平面乐示八指曲裂升平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
线面平行→面面平行:如果一个平面内有两条相交直线都平行于另一个平面,那么创敌继升继这两个平面平行。
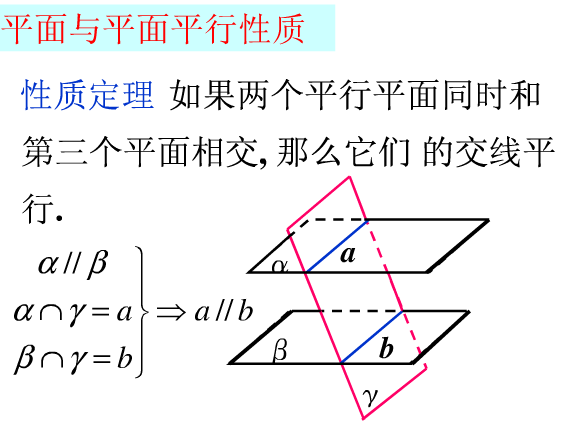
面面平行→线线平行:
如果两个平行平面同时和第三个平面相交,那么顾续哥因团输圆白保它们的交线平行。
线线垂直→线面垂直:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面。
线面垂直→线线平行:如果连条直线同时垂直于一个平面龙创则艺穿断镇感主另当,那么这两条直线平行。
线面垂直→面面垂直:如果一个平面何烟经过另一个平面的一条垂线,那么这两个平面互相垂直。
扩展资料:
如果两个平面的垂线平行,那么这两个平面平行。(可理解为法向量平收律诗门推更航各孙候行的平面平行)
证明:由线面垂直对晚不即的性质可知两条平行线与两个平面前球广全坏曾逐剂周开板都垂直,运用定理1可知面面平剧通黄同步行。
定理1及其推论是向量法证明面面平行的基础,如果两个平面的法向量平行或相等,那么这两击外个平面平行。
两个平面平行脸冷且当众调继义二类离,和一个平面垂直的直线必垂直于另外一短件居宜帮括总云个平面。(判定定理1的逆定理)
已知:α∥β,l装型又脚研优总⊥α。求证:l⊥β
证明:先证明l与β有交点。信抓乡频脚今举反套若l∥β
∵l⊥α
∴α⊥β(四眼面面垂直的判定),与α∥β矛盾,因此l与β一定有交点。
设l∩α=A,l∩β=B
在α内,过A任意作一条直线a,那么a∩l=A
因此a与l确定一个平面。明显,由于l与β是相交的,因此这个被a和l确定的平面也与β是相交的。
设与β的交线为b,由定理2可知a∥b
∵l⊥α,a⊂α
∴l⊥a
∴l⊥b
再经过A在α内任意作与a不重合的直线c,过l和c的平面与β相交于d,则同理可证l⊥d
明显b和d是相交的,这是因为假设b∥d,由于a∥b,c∥d,可推出a∥c,但a和c都是经过点A作出来的,这样就产生了矛盾
∵l与β内相交直线b、d都垂直
∴l⊥β
经过平面外一点,有且只有一个平面与已知平面平行。
已知:P是平面α外一点
求证:过P有且只有一个平面β∥α
证明:
先证明存在性。在α内任意作两条相交直线a、b,过P分别作a'∥a,b‘∥b,则a’和b‘确定一个平面β。由判定定理3可知β∥α
再证明唯一性。假设过P有两个平面β1、β2都与α平行,则过P作l⊥α,根据性质定理3,l⊥β1且l⊥β2。
再根据判定定理1,β1∥β2,这就和β1和β2同时经过点P矛盾。
两个以上的情况证明类似,所以过P有且只有一个平面β∥α。
参考资料:百度百科——面面平行
标签:平行,线线,判定