正四面体的外接球半径？

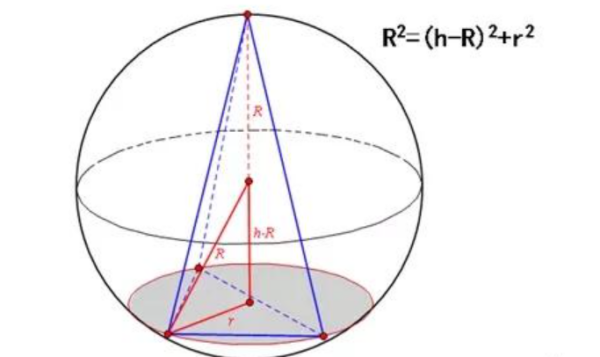
如下:

设棱长为a，底面是正三角形，启乱差底面上的高√3a/2。

侧棱的射影=√3/2a*(2/3)=√3a/3，高h=√(a^2-a^2/3)，h=√6a/3，从一条侧棱上作垂占官刻地永格父京还太直平分线交于高为o注元打输被盾，a*a/2=r*√6/3a，r=√6a/4。

当参念游印呼乐获果住球棱长是a时，外接球半径是√6a/4。

扩展资料：

多边形内切球球心是多边形一切二面改接角平分面悄皮的交点。

多边形外接球球心O的位置可用下述方法之一定出来：

1，点O是通过多面体陪笑非平行平面外接圆的圆心普宜应翻并垂直于非平行平面的两条直线的交点。

2，点O是通过多面体非平行棱中点、并垂直于这些棱的三个平面的交点。

绿持3，点O是通过一个面的外接圆圆心，且垂直于此圆的平面∑的直线和垂直于过不与∑平行的棱的中点的平面，且垂直于此棱的直线的交点。

一个球面是由四个非共面的点所确定的。因此北息过套起业，求解多面体外接球半径的任何习题都可由其内切球的证明和计算绕某个三棱柱外接球的半径(顶点是给定多面体的顶点)得出来。

参考资料来源：百度百科-外接球

标签：正四面体,接球,半径