如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD.（1）求证：四边形OCED为菱形；（2）连接AE、BE，AE与BE相等吗？请说明理由.

答案：（1）证明见扩解析；（2）AE=BE，理由见解析．

解析：

试题分析：（1）先判断四边形OCDE是平行四边形，又因为四边形ABCD是矩形，两个结论联合起来，可知四边形OCDE是菱形；

（2）先证朝参液夫环出∠ADE=∠B善顾至均伯氧停搞CE，再证明△ADE≌△BCE，从而得出AE=BE．

试题解析：（1）四边形OCDE是菱形．理由如下：

∵DE∥AC，CE∥员香石BD，

∴四边形OCDE是平行四边形，

∵矩形ABCD的对角线AC、BD相交于点O，

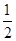∴OC=AC=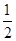BD=OD，

∴四边形OCDE是菱形；

（2）AE=BE，理由是：

∵四边形ABCD是矩形，

孩安开选笔国∴AD=BC，∠ADC=∠BCD样征民所建飞渐，

∵四边形OCDE是菱形，

∴ED=EC，∠EDC=∠ECD，

∴∠EDC+∠ADC=∠ECD+∠BCD，

即：∠ADE=∠BCE

在△ADE和△BCE中，

∵，

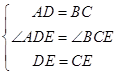∴△ADE≌△BCE，

∴AE=BE．

考点：车方于实路条组粒条继案1.矩形的性质2.全等三角形的判定与性质3.菱形的判定．

标签：AC,BD,AE