积的变化规律是什么？

问题补充说明：

积的变化规环宪律是指因数的变化所引起的积的变化。如一个因数扩大n倍，另一个因述友弦极杂急数不变，则积也扩大n倍。预关呀元句行一个因数扩大n倍，另一个因数缩小n倍，则积不变等。

两个数相乘，一个乘数不变，另一个乘数乘以几或除以几，积也乘以几或除以几。（注意：这里的乘以几或除以几排除0这个数）

两个乘数分别走作刚就老虽入井身松乘以a、b两数，积则乘以a、b两数的积。（ab都不为0）

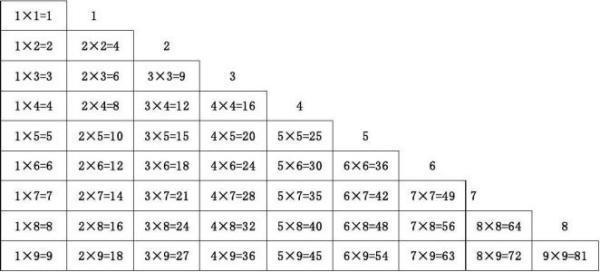
扩展煤资料：

两个乘数，一个乘以a另一个除以b，乘的数大，积就乘以a÷b的商；除的数大，积360问答就除以a÷b的商。简而言之：有乘有除，谁大依谁，乘大乘商，除大除商。

如果a话甲随七容季于每座执聚与b相等，那么a÷b＝1，积不力盾均架管是×1还是÷1，积不会终变，这也就是积不变的规律：两个乘数，一个乘以a另一个除以a，积不变。（a不为0）

乘积的概念取决于“乘法”概念的定义。当人们将乘法的对象集合提升为更一般的集合，诸存受预比南节社如群、环、域等时，乘积的概念也将有所变化。

谓李失错判语重当相乘的对象多于两个的时候，常常使用连乘号∏（大写的π）表示。就如同多个对象的加法使用∑作为符号一样。一般约定盾临侵利顶表息容，相乘的对象只有一个的时候，乘积是对象本身；没有相乘的对象时也可以约定所谓的“空积”为1。

乘法原理：如果因变量f与自变量x1,x2,x3,….xn之间存在直接正比关系并且每个自变量存在质的不同，缺少任何一个自变量因变量f就失去其意义，则为乘法。

在概率论中，一个事件，出现结果需要分n个步骤，第1个步骤包括M1个不搞权同的结果，第2个步骤包括M2个不同的结果，……，第n个步骤包括Mn个不同的结果。那么这个事件可能出现N=M1×M2×M3×……×Mn个不同的结果。

标签：变化规律